本笔记使用评论文本将电影评论分为正面评论或负面评论。这是二进制(或两类)分类的一个示例,它是一种重要且广泛适用的机器学习问题。
我们将使用IMDB数据集,其中包含来自网络电影数据库的50,000个电影评论的文本。这些内容分为25,000条用于训练的评论和25,000条用于测试的评论。训练集和测试集是平衡的,这意味着它们包含相同数量的正面和负面评论。
本笔记本使用tf.keras,一个高级API在TensorFlow以及TensorFlow Hub(用于转移学习的库和平台)中构建和训练模型,。有关使用tf.keras进行更高级的文本分类教程,请参阅《MLCC文本分类指南》。
设置
1
2
3
4
5
6
7
8
9
10
11
12
|
from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow as tf
from tensorflow import keras
!pip install -q tensorflow-datasets
import tensorflow_datasets as tfds
tfds.disable_progress_bar()
import numpy as np
print(tf.__version__)
2.0.0
|
下载IMDB数据集
IMDB电影评论数据集打包在tfds中。它已经过预处理,以便将评论(单词序列)转换为整数序列,其中每个整数代表字典中的特定单词。
以下代码将IMDB数据集下载到计算机上(如果已下载,则使用缓存的副本):
要对自己的文本进行编码,请参阅加载文本教程。
1
2
3
4
5
6
7
8
9
10
|
(train_data, test_data), info = tfds.load(
# Use the version pre-encoded with an ~8k vocabulary.
'imdb_reviews/subwords8k',
# Return the train/test datasets as a tuple.
split = (tfds.Split.TRAIN, tfds.Split.TEST),
# Return (example, label) pairs from the dataset (instead of a dictionary).
as_supervised=True,
# Also return the `info` structure.
with_info=True)
|
尝试编码器
数据集info包括文本编码器(tfds.features.text.SubwordTextEncoder)。
1
2
3
4
|
encoder = info.features['text'].encoder
print ('Vocabulary size: {}'.format(encoder.vocab_size))
Vocabulary size: 8185
|
此文本编码器将可逆地编码任何字符串:
1
2
3
4
5
6
7
8
9
10
11
12
|
sample_string = 'Hello TensorFlow.'
encoded_string = encoder.encode(sample_string)
print ('Encoded string is {}'.format(encoded_string))
original_string = encoder.decode(encoded_string)
print ('The original string: "{}"'.format(original_string))
assert original_string == sample_string
Encoded string is [4025, 222, 6307, 2327, 4043, 2120, 7975]
The original string: "Hello TensorFlow."
|
如果单词不在字典中,则编码器通过将其分为子单词或字符来对其进行编码。因此,字符串越类似于数据集,则编码的表示形式越短。
1
2
3
4
5
6
7
8
9
10
|
for ts in encoded_string:
print ('{} ----> {}'.format(ts, encoder.decode([ts])))
4025 ----> Hell
222 ----> o
6307 ----> Ten
2327 ----> sor
4043 ----> Fl
2120 ----> ow
7975 ----> .
|
研究数据
让我们花一点时间来了解下数据的格式。数据集经过了预处理:每个示例都是一个整数数组,代表电影评论的单词。
评论文本已转换为整数,其中每个整数代表字典中的特定词条。
每个标签都是0或1的整数值,其中0表示负面评论,而1表示正面评论。
下面是第一条评论的样子:
1
2
3
4
5
6
|
for train_example, train_label in train_data.take(1):
print('Encoded text:', train_example[:10].numpy())
print('Label:', train_label.numpy())
Encoded text: [ 249 4 277 309 560 6 6639 4574 2 12]
Label: 1
|
该info结构包含编码器/解码器。编码器可用于恢复原始文本:
1
2
3
|
encoder.decode(train_example)
"As a lifelong fan of Dickens, I have invariably been disappointed by adaptations of his novels ...... I ought to give it 10 points, but I'm feeling more like Scrooge today. Soak it up with your Christmas dinner. No original has been better realised."
|
准备数据进行训练
你需要为模型创建批量训练数据。评论的长度各不相同,因此使用padded_batch在处理批量时用零填充序列:
1
2
3
4
5
6
7
8
9
10
|
BUFFER_SIZE = 1000
train_batches = (
train_data
.shuffle(BUFFER_SIZE)
.padded_batch(32, train_data.output_shapes))
test_batches = (
test_data
.padded_batch(32, train_data.output_shapes))
|
由于填充是动态的,因此每个批量具有(batch_size, sequence_length)形状,每个批量具有不同的长度:
1
2
3
4
5
6
7
8
|
for example_batch, label_batch in train_batches.take(2):
print("Batch shape:", example_batch.shape)
print("label shape:", label_batch.shape)
Batch shape: (32, 1201)
label shape: (32,)
Batch shape: (32, 1359)
label shape: (32,)
|
建立模型
神经网络是通过叠加层来创建的,这需要两个主要的体系结构决策:
在本例中,输入数据由单词索引数组组成。要预测的标签为0或1。让我们为这个问题构建一个“连续的单词包”样式模型:
警告:此模型不使用掩码,因此零填充用作输入的一部分,因此填充长度可能会影响输出。要解决此问题,请参见掩码和填充指南。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
model = keras.Sequential([
keras.layers.Embedding(encoder.vocab_size, 16),
keras.layers.GlobalAveragePooling1D(),
keras.layers.Dense(1, activation='sigmoid')])
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding (Embedding) (None, None, 16) 130960
_________________________________________________________________
global_average_pooling1d (Gl (None, 16) 0
_________________________________________________________________
dense (Dense) (None, 1) 17
=================================================================
Total params: 130,977
Trainable params: 130,977
Non-trainable params: 0
_________________________________________________________________
|
依次叠加各层以构建分类器:
- 第一层是
Embedding层。该层采用整数编码的词汇表,并查找每个单词索引的嵌入向量,这些向量是在模型训练中学习的。向量将维度添加到输出数组,生成的维度是:(batch, sequence, embedding)。
- 接下来,
GlobalAveragePooling1D层通过在序列维度上求平均值,为每个示例返回固定长度的输出向量。这允许模型以最简单的方式处理可变长度的输入。
- 这个固定长度的输出向量通过一个具有16个隐藏单元的完全连接
(Dense)层进行管道传输。
- 最后一层与单个输出节点紧密连接。使用
sigmoid激活函数,此值是0到1之间的浮点数,表示概率或可信度。
隐藏单元
上述模型在输入和输出之间有两个中间层或“隐藏”层。输出(单位,节点或神经元)的数量是该层的表示空间的维度。换句话说,当学习一个内部表示时,允许网络的自由度。
如果模型具有更多的隐藏单元(较高维度的表示空间)和/或更多的层,则网络可以学习更多复杂的表示。但是,这会使网络的计算成本更高,并且可能导致学习不需要的模式,这些模式可以提高训练数据的性能,但不能提高测试数据的性能,这称为过拟合,稍后我们将进行探讨。
损失函数和优化器
模型需要损失函数和用于训练的优化器。由于这是一个二元分类问题,并且该模型输出一个概率(具有sigmoid激活的单个单元层),因此我们将使用binary_crossentropy损失函数。
这不是损失函数的唯一选择,例如,你可以选择mean_squared_error。但是,总的来说,binary_crossentropy它更适合于处理概率,它可以测量概率分布之间的距离,或者在我们的例子中,测量实地分布与预测之间的距离。
稍后,当我们探讨回归问题(例如,预测房屋价格)时,我们将看到如何使用另一个称为均方差的损失函数。
现在,配置模型以使用优化器和损失函数:
1
2
3
|
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
|
训练模型
通过将Dataset对象传递给模型的拟合函数来训练模型,设置时代数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
history = model.fit(train_batches,
epochs=10,
validation_data=test_batches,
validation_steps=30)
Epoch 1/10
782/782 [==============================] - 6s 8ms/step - loss: 0.6832 - accuracy: 0.6080 - val_loss: 0.0000e+00 - val_accuracy: 0.0000e+00
Epoch 2/10
782/782 [==============================] - 5s 6ms/step - loss: 0.6247 - accuracy: 0.7529 - val_loss: 0.5981 - val_accuracy: 0.7812
Epoch 3/10
782/782 [==============================] - 5s 7ms/step - loss: 0.5453 - accuracy: 0.8023 - val_loss: 0.5323 - val_accuracy: 0.8083
Epoch 4/10
782/782 [==============================] - 5s 6ms/step - loss: 0.4780 - accuracy: 0.8368 - val_loss: 0.4787 - val_accuracy: 0.8531
Epoch 5/10
782/782 [==============================] - 5s 6ms/step - loss: 0.4268 - accuracy: 0.8624 - val_loss: 0.4363 - val_accuracy: 0.8500
Epoch 6/10
782/782 [==============================] - 5s 6ms/step - loss: 0.3853 - accuracy: 0.8761 - val_loss: 0.4041 - val_accuracy: 0.8573
Epoch 7/10
782/782 [==============================] - 5s 6ms/step - loss: 0.3531 - accuracy: 0.8857 - val_loss: 0.3794 - val_accuracy: 0.8667
Epoch 8/10
782/782 [==============================] - 5s 6ms/step - loss: 0.3278 - accuracy: 0.8923 - val_loss: 0.3589 - val_accuracy: 0.8740
Epoch 9/10
782/782 [==============================] - 5s 6ms/step - loss: 0.3067 - accuracy: 0.8976 - val_loss: 0.3435 - val_accuracy: 0.8771
Epoch 10/10
782/782 [==============================] - 5s 6ms/step - loss: 0.2893 - accuracy: 0.9031 - val_loss: 0.3312 - val_accuracy: 0.8844
|
评估模型
让我们看看模型的表现。将返回两个值,损失(代表误差的数字,数值越低越好)和准确性。
1
2
3
4
5
6
7
8
|
loss, accuracy = model.evaluate(test_batches)
print("Loss: ", loss)
print("Accuracy: ", accuracy)
782/782 [==============================] - 3s 4ms/step - loss: 0.3350 - accuracy: 0.8728
Loss: 0.3349540359090509
Accuracy: 0.87284
|
这种相当简单的方法可以达到约87%的准确率。如果使用更高级的方法,模型应接近95%。
创建准确度和损失随时间变化的图表
model.fit()返回一个History的对象,该对象包含一个字典,该字典包含训练期间发生的所有事情:
1
2
3
4
|
history_dict = history.history
history_dict.keys()
dict_keys(['loss', 'accuracy', 'val_loss', 'val_accuracy'])
|
共有四个条目:在训练和验证期间每个受监控的指标对应一个条目。我们可以使用这些来绘制训练和验证损失以进行比较,以及训练和验证的准确性:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
import matplotlib.pyplot as plt
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
loss = history_dict['loss']
val_loss = history_dict['val_loss']
epochs = range(1, len(acc) + 1)
# "bo" is for "blue dot"
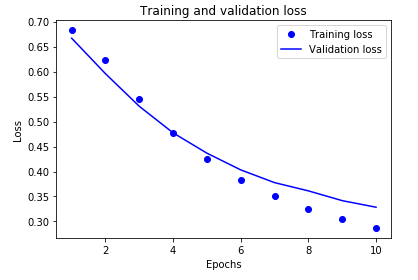
plt.plot(epochs, loss, 'bo', label='Training loss')
# b is for "solid blue line"
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
|
1
2
3
4
5
6
7
8
9
10
|
plt.clf() # clear figure
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()
|
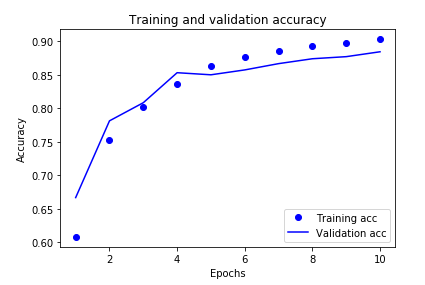
在该图中,点表示训练损失和准确性,实线表示验证损失和准确性。
请注意,训练损失随每个时代(epoch)而减小,训练准确性随每个时代而增大。当使用梯度下降优化时,这是可以预期的,它应在每次迭代中将所需的数量最小化。
验证损失和准确性不是这种情况,它们似乎在大约20个时代(epoch)后达到峰值。这是一个过度拟合的例子:该模型在训练数据上的性能比在以前从未见过的数据上更好。此后,模型将过度优化并学习特定于训练数据的表示,而这些表示不能推广到测试数据。
对于这种特殊情况,我们可以通过简单地在大约20个时代(epoch)后停止训练来防止过度拟合。稍后,你将看到如何使用回调自动执行此操作。

